Лекция 22.

эволюционно-синергетическая парадигма

 

4.  Бифуркации и управляющие параметры

 

Поведение системы, в которой происходит самоорганизация, удобно рассматривать с помощью бифуркационной диаграммы. По оси абсцисс диаграммы откладывается значение управляю­щего параметра, который характеризует воздействие, выводя­щее систему из равновесного состояния, а по оси ординат — па­раметр порядка, описывающий состояние системы и чувстви­тельный к возникновению в ней структуры.

(1)            Выше было сказано, что нелинейная система уравнений, которой описывается практически любая реальная сложная система, имеет не одно, а подчас целый спектр решений. Ответвления от известного решения появляются при изменении значения управляющих параметров системы. Изменения управляющих параметров способны вызвать катастрофические, т.е. большие скачки  переменных системы, и эти скачки осуществляются практически мгновенно.

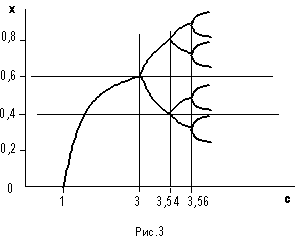
(2)            Путь на изолированном острове выводятся летом насекомые численностью x_j и откладывают яйца. Потомство их на следующее лето появится численностью x_{j+1  =}  cx_j (1- x_j )_­.  Рост популяции насекомых описывается первым членом в правой части уравнения x_j, а убыль – вторым. Параметр роста (коэффициент пропорциональности) с является управляющим параметром. При с<1  популяция при увеличении j убывает и исчезает. В области 1<c<3 численность приближается к значению x = 1 - (1/c). Следующий диапазон 3<c<3,4 соответствует двум ветвям решения и при определенных условиях численность может колебаться между ними (рис. 3). Т.е. она растет резко от малого значения, и откладывается много яиц. Но перенаселенность, возникающая на следующий год, вновь снижает численность в следующем году до малого значения., так что период колебания численности равен двум годам. Далее, при 3,4<c<3,54 имеем уже 4 ветви, и возникает 4—стадийный цикл колебаний и. т.д. Подобные решения имеют место для широкого класса систем химических, электрических, гидродинамических и т.д.

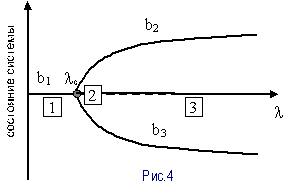
(3)            Итак, при изменении управляющих параметров в системе наблюдаются различные переходные явления, которые мы рассмотрим с помощью т.н. диаграммы бифуркации (см. рис. 4).

1 – асимптотическая ветвь, где система остается устойчивой, т.е. при малых l имеет одно единственное решение

2 – точка, где l=l_С  - здесь происходит потеря устойчивости. Появляется два решения.

3 – система вновь находится в равновесии, причем существуют 2 устойчивые ветви b1 и b2.

(14)         Сама точка l_С носит название точки бифуркации (<лат. раздвоение, размножение) или «точкой катастрофы».

(15)         Ранее уже использовалось понятие флуктуации, т.е. отклонение какой-либо величины от среднего значения. Здесь, как видим, малая флуктуация управляющего параметра может иметь определяющее значение для системы (она начинает развиваться либо по ветви b1, либо по ветви b2). В биологической эволюции флуктуации проявляются в мутациях, изменчивости, в то время как устойчивость обусловлена естественным отбором.

(16)         Усложнение структуры и поведения системы тесно связано с появлением новых путей решения в результате бифуркаций.   В сильно неравновесных условиях процессы самоорганизации соответствуют «тонкому взаимодействию» между  случайностью и необходимостью, флуктуациями и детерминистскими законами. Вблизи бифуркаций, т.е. резких, «взрывных» изменений системы, основную роль играют флуктуации или случайные элементы, тогда как в интервалах между бифуркациями преобладает детерминизм.

(17)         Поведение самоорганизующейся системы вблизи точки бифуркации характеризуется следующими закономерностями.

(18)          

 

(19)         Ситуацию, возникающую после воздействия флуктуации на систему и возникновения новой структуры,  И. Пригожин назвал порядком через флуктуацию или «порядком из хаоса». Флуктуации могут усиливаться в процессе эволюции системы или затухать, что зависит от эффективности «канала связи» между системой и внешним миром.

1.