Лекция 22.

эволюционно-синергетическая парадигма

 

1. Динамический хаос

 

В молекулярно-кинетической теории (МКТ) впервые была нарисована картина хаотического движения, которое не описывается никакой простой закономер­ностью. Любая попытка рассчитать точные траектории молекул газа оказывается безуспешной ввиду чрезвычайной чувстви­тельности результатов расчета к самому ничтожному изменению начальных условий. Единственно полезная информация о такой системе сводится к значениям вероятностей тех или иных ее состояний и средним значениям характерных физических вели­чин.

Эта картина радикально отличалась, например, от ньютонов­ской картины закономерного, предсказуемого дви­жения планет по своим орбитам. Вначале полагали, что причина такого отличия заключена лишь в очень большом количестве частиц в молекулярных системах. Считалось, что система, описываемая небольшим чис­лом уравнений, всегда ведет себя «хорошо», упорядоченно, а хаотическое поведение возникает с ростом числа элементов сис­темы, когда мы, вследствие ограниченности своих возможно­стей, более не способны отследить все взаимодействия в ней.

Однако, в XX веке выяснилось, что хаотическим, непредсказуемым поведением могут обладать и системы из очень небольшого числа частиц, например, трех. Была рассмотрена, в частности, следующая задача.

В систему двух одинаковых звезд, обращающихся друг во­круг друга, влетает астероид. Требуется вычислить его дальней­шую траекторию. Можно записать уравнения движения астероида, составить компьютерную программу для их решения. Однако дать общую характеристику движения невоз­можно: в зависимости от начальных условий, астероид либо вечно кружится в окрестности одной из звезд, либо время от времени перескакивает от одной звезды к другой, либо, в конце концов, навсегда покидает звездную систему. Переход от одного типа поведения к другому может происходить при ничтожном изменении начальных условий. Поскольку же они всегда из­вестны с некоторой погрешностью, это и означает непредска­зуемость движения астероида.  

Таким образом, возникает парадокс: математически задача полностью определена, возможность ее решения, как теоретиче­ская, так и практическая, имеется, а дать долгосрочный прогноз поведения системы невозможно.

Ситуация, когда поведение простой системы невозможно предсказать из-за ее чувствительности к слабому изменению начальных условий, называется динамическим хаосом.

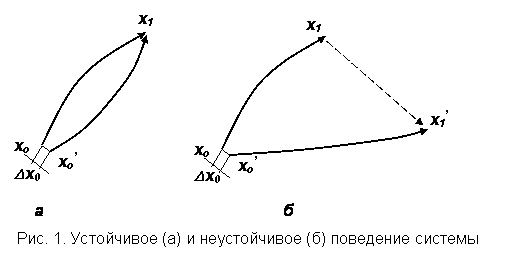
Чувствительность к изменению начальных условий характерна для неустойчивых систем и может быть проиллюстрирована рис. 1, где х_о – начальное состояние системы, Dх₀ – малое изменение начальных условий, х_о^’ – начальное состояние  после внесения малого изменения. При начальном состоянии х_о система через время t система должна прийти в состояние х_{1 .} Если система устойчива, то со временем, она «гасит» внесенное возмущение, и ее поведение приближается к  х_1. Для неустойчивых, чувствительных к слабым возмущениям (флуктуациям) систем ситуация иная (рис.1б). Малое отклонение начального состояния приводит систему в качественно иное состояние x₁^’ .

Хаос следует отличать от беспорядка. Беспорядочным называют поведение, определяемое постоянно действующими факторами, которые мы не можем или не хотим учитывать.

Так, броуновское движение частицы порошка в жидкости беспорядочно, поскольку полностью обусловлено невидимыми для наблюдателя ударами молекул по частице. Хаотическое же поведение возникает, когда все определяющие его факторы из­вестны, но воспользоваться этим знанием невозможно из-за чрезвычайной чувствительности расчетов к малым ошибкам.

Системы с динамическим хаосом. Динамический хаос проявляется во многих ситуациях. Так, уста­новлено, что хаотична динамика Солнечной системы: вследст­вие взаимного притяжения планет друг к другу медленно изме­няются параметры их орбит, и невозможно предсказать, каковы они будут через сотни миллионов лет.

В начале 60-х годов XX века американский метеоролог Э, Лоренц вывел систему трех уравнений, описывающую изменение погоды над ограниченным участком земной поверхности, и обнару­жил, что она обладает динамическим хаосом. Хаотично, как вы­яснилось, поведение атмосферы в целом — и потому долгосроч­ный (на месяцы вперед) прогноз погоды никогда не станет точ­ным, как бы ни росла мощность компьютеров в метеоцентрах.

Электрическая активность головного мозга также хаотична. В обеспечении психической деятельности участвует множество мозговых структур, объединяясь в ансамбли, модули, блоки, функциональные системы. Для всех этих систем характерна, выраженная в той или иной степени, периодическая активность. Электрическая активность мозга представляет собой сложный процесс, несущий отчетливые признаки хаоса, характеризующие нормальную активность мозга. Существует мнение, что хаос, возможно, играет роль генератора, обеспечивающего быструю адаптацию мозга к меняющимся условиям.

В послед­ние десятилетия выяснилось, что колебания курсов акций на фондовых рынках, по всей видимости, также хаотичны (не бес­порядочны!). Другими словами, в принципе возможно найти систему уравнений (от 5 до 7), которая описывает, как курсы акций меня­ются с течением времени, но даже с помощью этой сис­темы невозможно предсказать, каков будет индекс Доу-Джонса, скажем, через пару лет.

Однако, динамический хаос несет в себе «зародыши» порядка, другими словами, в хаотических системах создаются условия для образования упорядоченных структур, т.е. самоорганизации.