Молекулярно-кинетическая теория впервые показала
несостоятельность механического детерминизма и плодотворность статистического,
вероятностного подхода в отношении систем, состоящих из большого числа частиц.
Действительно, было подсчитано, что ошибка величиной 10-100 в
определении начальных положений или скоростей молекул одного моля спустя
секунду приведет к тому, что их траектории не будут иметь ничего общего с расчетными.
В молекулярно-кинетической теории появился совершенно
новый подход к описанию состояния системы. Состояние описывалось теперь не
значениями физических величин, а вероятностями
этих значений. Этот подход оказался чрезвычайно плодотворным при построении
фундаментальных естественнонаучных теорий XX
века.
1. Динамический хаос
В
молекулярно-кинетической теории (МКТ) впервые была нарисована картина хаотического
движения, которое не описывается никакой простой закономерностью. Любая попытка рассчитать
точные траектории молекул газа
оказывается безуспешной ввиду чрезвычайной чувствительности результатов расчета к
самому ничтожному изменению начальных
условий. Единственно полезная информация о такой системе сводится к значениям вероятностей
тех или иных ее состояний и средним значениям характерных физических
величин.
Эта картина радикально
отличалась, например, от ньютоновской картины закономерного, предсказуемого
движения планет по своим орбитам. Вначале полагали, что причина такого отличия
заключена лишь в очень большом количестве частиц в молекулярных системах. Считалось,
что система, описываемая небольшим числом уравнений, всегда ведет себя
«хорошо», упорядоченно, а хаотическое поведение возникает с ростом числа
элементов системы, когда мы, вследствие ограниченности своих возможностей,
более не способны отследить все взаимодействия в ней.
Однако, в XX веке
выяснилось, что хаотическим, непредсказуемым поведением могут обладать и
системы из очень небольшого числа частиц, например, трех. Была рассмотрена, в
частности, следующая задача.
В систему двух
одинаковых звезд, обращающихся друг вокруг друга, влетает астероид. Требуется
вычислить его дальнейшую траекторию. Можно записать уравнения движения астероида,
составить компьютерную программу для их решения. Однако дать общую характеристику
движения невозможно: в зависимости от начальных условий, астероид либо вечно
кружится в окрестности одной из звезд, либо время от времени перескакивает от
одной звезды к другой, либо, в конце концов, навсегда покидает звездную
систему. Переход от одного типа поведения к другому может происходить при
ничтожном изменении начальных условий. Поскольку же они всегда известны с
некоторой погрешностью, это и означает непредсказуемость движения астероида.
Таким образом, возникает
парадокс: математически задача полностью определена, возможность ее решения,
как теоретическая, так и практическая, имеется, а дать долгосрочный прогноз
поведения системы невозможно.
Ситуация, когда
поведение простой системы невозможно предсказать из-за ее чувствительности к
слабому изменению начальных условий, называется динамическим хаосом.
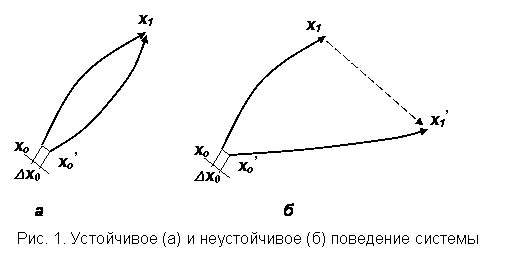
Чувствительность к изменению
начальных условий характерна для неустойчивых систем и может быть проиллюстрирована
рис. 1, где хо – начальное состояние системы, Dх0 – малое
изменение начальных условий, хо’ – начальное
состояние после внесения малого изменения.
При начальном состоянии хо система через время t система должна прийти в состояние х1 . Если
система устойчива, то со временем, она «гасит» внесенное возмущение, и ее поведение
приближается к х1. Для
неустойчивых, чувствительных к слабым возмущениям (флуктуациям) систем ситуация
иная (рис.1б). Малое отклонение начального состояния приводит систему в качественно
иное состояние x1’ .
Хаос следует отличать от
беспорядка. Беспорядочным называют поведение, определяемое
постоянно действующими факторами, которые мы не можем или не хотим учитывать.
Так, броуновское
движение частицы порошка в жидкости беспорядочно, поскольку полностью
обусловлено невидимыми для наблюдателя ударами молекул по частице. Хаотическое
же поведение возникает, когда все определяющие его факторы известны, но
воспользоваться этим знанием невозможно из-за чрезвычайной чувствительности
расчетов к малым ошибкам.
Системы с динамическим хаосом. Динамический хаос проявляется во многих ситуациях. Так, установлено,
что хаотична динамика Солнечной системы: вследствие взаимного притяжения
планет друг к другу медленно изменяются параметры их орбит, и невозможно
предсказать, каковы они будут через сотни миллионов лет.
В начале 60-х годов XX века
американский метеоролог Э, Лоренц вывел систему трех уравнений, описывающую
изменение погоды над ограниченным участком земной поверхности, и обнаружил,
что она обладает динамическим хаосом. Хаотично, как выяснилось, поведение
атмосферы в целом — и потому долгосрочный (на месяцы вперед) прогноз погоды
никогда не станет точным, как бы ни росла мощность компьютеров в метеоцентрах.
Электрическая активность
головного мозга также хаотична. В обеспечении психической деятельности участвует
множество мозговых структур, объединяясь в ансамбли, модули, блоки,
функциональные системы. Для всех этих систем характерна, выраженная в той или
иной степени, периодическая активность. Электрическая активность мозга
представляет собой сложный процесс, несущий отчетливые признаки хаоса, характеризующие
нормальную активность мозга. Существует мнение, что хаос, возможно, играет роль
генератора, обеспечивающего быструю адаптацию мозга к меняющимся условиям.
В последние десятилетия
выяснилось, что колебания курсов акций на фондовых рынках, по всей видимости,
также хаотичны (не беспорядочны!). Другими словами, в принципе возможно найти
систему уравнений (от 5 до 7), которая описывает, как курсы акций меняются с течением
времени, но даже с помощью этой системы невозможно предсказать, каков будет индекс
Доу-Джонса, скажем, через пару лет.
Однако, динамический
хаос несет в себе «зародыши» порядка, другими словами, в хаотических системах
создаются условия для образования упорядоченных структур, т.е. самоорганизации.
2. Концепция
самоорганизации в науке
(1)
На предыдущих лекциях при
рассмотрении самых различных вопросов из разных областей естествознания мы не
раз обращались к понятию самоорганизация, которое неразрывно связано с понятием
эволюции систем. Теперь возникает следующая проблема: каковы механизмы
самоорганизации этих систем? Концепция самоорганизации в настоящее время
приобретает все большее значения, становясь парадигмой исследования
обширного класса систем и процессов, происходящих в них. В 70-х годах 20-го
века возникло новое междисциплинарное научное направление – синергетика, которая изучает механизмы самоорганизации и развития. Областью ее исследований
является изучение эволюции различных структур, относительная устойчивость
которых поддерживается благодаря притоку энергии и вещества извне. В основе
синергетики лежит, среди прочих, важное утверждение о том, что материальные
системы могут быть закрытыми и закрытыми, равновесными и неравновесными,
устойчивыми и неустойчивыми, линейными и нелинейными, статическими и динамическими.
Принципиальная же возможность процессов
самоорганизации обусловлена тем, что в целом все живые и неживые,
природные и общественные системы являются открытыми, неравновесными, нелинейными.
Таким образом, синергетика – это междисциплинарное направление научных исследований, предмет которого
— общие закономерности самоорганизации
в природных и социальных системах.
Синергетика рассматривает системы самой
разнообразной природы: физические, химические, биологические, социальные,
процессы самоорганизации в которых, как выяснилось, описываются одними и теми
же математическими моделями и, следовательно, подчиняются универсальным
закономерностям.
(2)
Возникновение
синергетики связано, в основном, с именами И. Пригожина - бельгийского физика и химика И.Пригожина,
лауреата Нобелевской премии 1977 г., немецкого физика Г.Хакена, другого
немецкого ученого М. Эйгена, а также наших отечественных ученых Б. Белоусова и
Жаботинского.
(3)
И.Пригожин, разрабатывая
современную термодинамику необратимых процессов (неравновесную термодинамику)
открыл явление образования упорядоченных
структур из хаотического, неупорядоченного состояния системы, т.е. самоорганизацию
и сформулировал теорему о минимуме производства энтропии в стационарном
неравновесном состоянии. К своим идеям
он пришел, анализируя специфические химические реакции, которые впервые
экспериментально были изучены Б. Белоусовым и А. Жаботинским. И. Пригожин со своими сотрудниками
И.Стенгерс, Г.Николисом построили математическую модель таких реакций, а также
показали, что в сильно неравновесных условиях может совершаться переход от
беспорядка, теплового хаоса к порядку, организованности.
(4)
Г. Хакен, изучая
процессы самоорганизации, происходящие в лазере, пришел к выводу, что главной
особенностью процесса самоорганизации в любой системе является возникновение
согласованного, кооперативного поведения большого числа ее элементарных
подсистем. Он-то и назвал новое направление исследований синергетикой, что в
переводе с греческого означает совместное действие, или взаимодействие, и
хорошо передает смысл и цель нового подхода к изучению явлений.
(5)
М.Эйген доказал, что
открытый Ч. Дарвином принцип отбора справедлив и на микроуровне, а генезиз
(происхождение жизни есть результат процесса отбора, происходящего на
молекулярном уровне. Он показал, что сложные органические структуры с
адаптационными характеристиками возникают благодаря эволюционному процессу
отбора на основе автокатализа.
(6)
3. Необходимые условия
самоорганизации
Одно
из главных достижений синергетики — выяснение условий, выполнение которых
необходимо для начала самоорганизации в системе любой природы. Подчеркнем, что
эти условия — необходимые, то есть, если хотя бы одно из них не
выполнено, никаких упорядоченных структур в системе не возникнет наверняка. К
сожалению, до сих пор неизвестны достаточные условия, выполнение
которых гарантировало бы начало самоорганизации.
(1)
Порядок и хаос. В результате протекания процессов в
изолированных системах сами системы переходят в состояние равновесия, которое
соответствует максимальному беспорядку системы – равновесный тепловой хаос.
Таким образом, самоорганизация, или эволюция в случае замкнутой системы
приводит ее в состояние максимального беспорядка. В реальности, тем не менее,
часто наблюдаются совершенно противоположные явления.
(2)
Уже теория Канта и
Лапласа об образовании упорядоченной Солнечной системы из хаотических
туманностей противоречила II началу термодинамики. Но особенно ярко
проявилось противоречие II начала термодинамики с эволюционной теорией
Дарвина. Ведь согласно ей, в мире живого естественно протекающие процессы ведут
к усложнению форм и структур, к увеличению порядка, избавлению от хаоса и
удалению от равновесия. Другими словами, самоорганизация в живой природе приводит
систему к прямо противоположному состоянию, чем самоорганизация в неживых
системах. Все это привело к появлению понятия открытой системы, которое
и позволило устранить упомянутые противоречия.
(3)
Открытость систем. Такие понятия как изолированная (закрытая)
система, необратимые процессы являются идеализацией. При изучении обратимых
процессов (например, качание маятника в вакууме при отсутствии трения) нет
смысла говорить о направлении течения времени, т.к. прошлое, настоящее и
будущее в этом случае не отличаются. Поэтому в уравнениях обратимых процессов
время выступает всего лишь как параметр, который можно изменять. Но в
реальности в случае с маятником всегда присутствует трение, колебания маятника
будут затухающими, и прошлое, настоящее и будущее будут уже отличаться. Ранее
уже говорилось о том, что обратимых процессов в живой природе нет, и эволюционным
принципом стало II начало термодинамики, утверждающее, что энтропия
изолированной системы возрастает. Именно
рост энтропии устанавливает направление протекания процесса, т.е. «стрелу
времени».
(4)
В своей книге «Что такое
жизнь» выдающийся австрийский физик Э. Шредингер указал на то, что средство,
при помощи которого организм поддерживает себя на достаточно высоком уровне
упорядоченности, т.е. на достаточно низком уровне энтропии, в действительности
состоит в непрерывном извлечении упорядоченности из окружающей его среды.
Другими словами, организм извлекает из окружающей среды негэнтропию. Открытая
система заимствует энергию и вещество из окружающей его среды и одновременно
выводит в окружающую среду отработанное вещество и отработанную энергию. Вырабатывая
и заимствуя энергию, открытая система производит энтропию, но она
не накапливается в ней, а выводится в окружающую среду. С поступлением
энергии и вещества в открытую систему ее неравновесность возрастает,
разрушаются прежние связи между элементами и возникают новые, которые приводят
к новой структуре, новым кооперативным процессам, т.е. к коллективному поведению ее элементов.
(5)
Отсюда первое условие самоорганизации:
|
Система
должна быть открытой |
(6)
Второе условие самоорганизации:
|
Система
должна быть неравновесной |
(7)
Основным признаком
неравновесности является протекание сквозь систему потоков энергии и
вещества, вызываемых температурными, химическими и иными градиентами (градиент
— это мера неоднородности распределения той или иной величины, ее перепад). Так,
кухня, в которой на плите стоит только что вскипевший чайник, — неравновесная
система, поскольку между чайником и окружающим воздухом имеется градиент
температуры. Благодаря ему возникает направленный поток тепловой энергии, и
чайник остывает. Однако когда температура чайника сравняется с температурой
окружающего воздуха, равновесие все еще не будет достигнуто. Дело в том, что
концентрация воды в чайнике больше концентрации водяного пара в воздухе (химический
градиент), что приводит к направленному потоку молекул воды из чайника. Через
несколько дней вся вода из чайника испарится и можно будет считать состояние равновесия
достигнутым.
(8)
Неравновесная система
может быть и замкнутой, не сообщающейся с внешним миром. Например, не исключено,
что наша Вселенная — изолированная система. Но масштабы ее таковы, что время,
необходимое для ее перехода в равновесное состояние, каким бы оно ни было,
астрономически велико. Однако чаще всего длительное поддержание системы в
неравновесном (тем более, сильно неравновесном, см. ниже) состоянии требует,
чтобы она была незамкнутой и открытой.
(9)
Важно также отметить,
что система не просто должна быть неравновесной – она должна быть сильно
неравновесной, т.е. градиенты должны быть достаточно велики. Например,
живые организмы являются сильно неравновесными системами.
(10)
Физическая теория
неравновесных систем, неравновесная термодинамика, начала развиваться в
середине XIX века, однако в течение почти ста лет в ней считалось,
что все процессы в таких системах приводят лишь к разрушению структур,
сглаживанию неоднородностей. Лишь в середине XX века
стало понятно, что это справедливо только для слабо неравновесных систем, а
при сильном отклонении от равновесия неоднородности могут также и возникать,
приводя к образованию так называемых диссипативных структур.
(11)
Самоорганизация связана
также с ускорением производства энтропии, т.е. рассеянием энергии, или диссипацией.
(12)
Диссипативность. Великий
русский математик А.М.Ляпунов разработал общую теорию устойчивости состояний
систем. Очень кратко ее идею можно выразить следующим образом. Устойчивые
состояния систем не теряют своей устойчивости при флуктуациях физических параметров,
поскольку система за счет внутренних взаимодействий способна погасить
возникающие флуктуации. Неустойчивые системы, наоборот, при возникновении
флуктуаций способны усиливать их, и, в результате такого нарастания амплитуд
возмущений система уходит из стационарного состояния (рис.1). Критерием
эволюции при этом является величина прироста энтропии (dS/dt) < 0, которая указывает направление развития физической
системы к устойчивому стационарному состоянию. Эти процессы происходят достаточно
медленно, поэтому на каждом этапе как бы достигается равновесие. Величина прироста энтропии за единицу времени
в единице объема называется функцией диссипации, а системы, в
которых функция диссипации отлична от нуля, называются диссипативными. В таких
системах энергия упорядоченного движения переходит в энергию неупорядоченного
движения и, в конечном счете, в тепло. Практически все системы являются
таковыми, поскольку трение и прочие силы сопротивления приводят к диссипации
энергии (диссипация < лат. dissipatio – разгонять, рассеивать).
(13)
При определенных
условиях суммарное уменьшение энтропии за счет обмена потоками с внешней средой
может превысить ее внутреннее производство. Тогда неупорядоченное однородное
состояние системы может потерять устойчивость. В ней возникают и могут возрасти
до макроскопического уровня т.н. крупномасштабные флуктуации, т.е.
существенные отклонения описывающих ее параметров от их среднего значения. При
этом из хаоса могут возникнуть структуры, которые последовательно начнут
переходить во все более упорядоченные. Образование этих структур происходит не
из-за внешнего воздействия, а за счет внутренней перестройки системы, поэтому
это явление и получило название самоорганизации.
При этом энтропия, отнесенная к тому же значению энергии, убывает. Пригожин
назвал упорядоченные образования, возникающие в диссипативных системах в ходе
неравновесных необратимых процессов, диссипативными структурами.
(14)
Важно отметить
следующее:
|
При
возникновении упорядоченной структуры энтропия занимаемой ею области
понижается, а энтропия прилегающих областей возрастает. При этом суммарное
изменение энтропии неизменно оказывается положительным. |
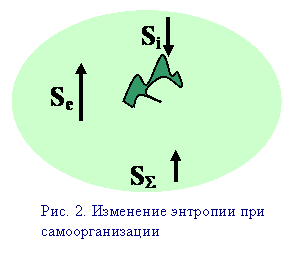
Более того, при возникновении новой упорядоченной структуры
скорость
изменения энтропии в занимаемой ею области пространства скачкообразно возрастает.
(15)
На макроуровне диссипативность
проявляется как хаос. На микроуровне хаос – это не разрушающий фактор, а сила,
выводящая систему на путь образования новых структур.
(16)
Третье необходимое условием самоорганизации:
|
Система
должна быть нелинейной |
(17)
Нелинейность. Сложные
системы являются нелинейными. Для их описания используются нелинейные математические
уравнения, т.е. уравнения, в которых искомые величины входят в степенях больше
единицы, в составе математических функций (тригонометрических, логарифмических
и т.п.) или коэффициенты зависят от свойств среды и особенностей протекания
процесса. Нелинейные уравнения могут иметь несколько качественно различных
решений. Физически это означает возможность различных путей эволюции системы.
|
Линейная система отличается тем, что ее реакция на несколько одновременных
воздействий равна
сумме реакций на каждое воздействие по отдельности |
|
Нелинейные
системы способны качественно изменять
свое поведение
при количественном изменении
воздействия. |
4.
Бифуркации и управляющие параметры
Поведение
системы, в которой происходит самоорганизация, удобно рассматривать с помощью бифуркационной диаграммы. По
оси абсцисс диаграммы откладывается значение управляющего параметра, который характеризует воздействие,
выводящее систему из равновесного состояния, а по оси ординат — параметр порядка, описывающий
состояние системы и чувствительный к возникновению в ней структуры.
(18)
Выше было сказано, что
нелинейная система уравнений, которой описывается практически любая реальная
сложная система, имеет не одно, а подчас целый спектр решений. Ответвления от
известного решения появляются при изменении значения управляющих параметров
системы. Изменения управляющих параметров способны вызвать катастрофические, т.е. большие скачки переменных системы, и эти скачки осуществляются
практически мгновенно.
|
|
(19)
Путь на изолированном
острове выводятся летом насекомые численностью xj и откладывают яйца. Потомство их на следующее лето
появится численностью xj+1 = cxj (1- xj ). Рост популяции насекомых
описывается первым членом в правой части уравнения xj, а убыль – вторым. Параметр роста (коэффициент пропорциональности)
с
является управляющим параметром. При с<1
популяция при увеличении j убывает и исчезает. В области 1<c<3 численность
приближается к значению x = 1 - (1/c).
Следующий диапазон 3<c<3,4 соответствует двум ветвям решения и при определенных
условиях численность может колебаться между ними (рис. 3). Т.е. она растет
резко от малого значения, и откладывается много яиц. Но перенаселенность,
возникающая на следующий год, вновь снижает численность в следующем году до
малого значения., так что период колебания численности равен двум годам. Далее,
при 3,4<c<3,54 имеем уже 4 ветви, и возникает 4—стадийный цикл
колебаний и. т.д. Подобные решения имеют место для широкого класса систем химических,
электрических, гидродинамических и т.д.
|
|
(20)
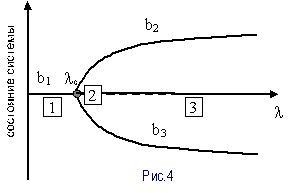
Итак, при изменении
управляющих параметров в системе наблюдаются различные переходные явления,
которые мы рассмотрим с помощью т.н. диаграммы бифуркации (см. рис. 4).
1 – асимптотическая ветвь, где система остается
устойчивой, т.е. при малых l имеет одно единственное решение
2 – точка, где l=lС - здесь происходит потеря устойчивости. Появляется
два решения.
3 – система вновь находится в равновесии, причем
существуют 2 устойчивые ветви b1 и b2.
(14)
Сама точка lС носит название точки
бифуркации (<лат. раздвоение, размножение) или «точкой катастрофы».
(15)
Ранее уже использовалось
понятие флуктуации, т.е. отклонение какой-либо величины от среднего значения.
Здесь, как видим, малая флуктуация управляющего параметра может иметь
определяющее значение для системы (она начинает развиваться либо по ветви b1,
либо по ветви b2). В биологической эволюции флуктуации проявляются в
мутациях, изменчивости, в то время как устойчивость обусловлена естественным
отбором.
(16)
Усложнение структуры и
поведения системы тесно связано с появлением новых путей решения в результате
бифуркаций. В сильно неравновесных
условиях процессы самоорганизации соответствуют «тонкому взаимодействию»
между случайностью и необходимостью,
флуктуациями и детерминистскими законами. Вблизи бифуркаций, т.е. резких,
«взрывных» изменений системы, основную роль играют флуктуации или случайные
элементы, тогда как в интервалах между бифуркациями преобладает детерминизм.
(17)
Поведение
самоорганизующейся системы вблизи точки бифуркации характеризуется следующими
закономерностями.
(18)
|
1. По мере
приближения к точке бифуркации флуктуации в системе нарастают; 2. Элементы
возникающей в точке бифуркации упорядоченной структуры формируются из
флуктуаций, случайно возникших до точки бифуркации. |
(19)
Ситуацию, возникающую
после воздействия флуктуации на систему и возникновения новой структуры, И. Пригожин назвал порядком через флуктуацию
или «порядком
из хаоса». Флуктуации могут усиливаться в процессе эволюции системы или
затухать, что зависит от эффективности «канала связи» между системой и внешним
миром.
1.